當施加力時彈簧變形並且在移除力時具有恢復其原始形狀的特性。彈簧的基本要求是，即使通過這種方式施力使其變形，也具有試圖恢復原狀的性質，這是必要條件。能夠回到原來的形狀, 被稱為 "恢復力", 恢復力的存在被列為彈簧的一大特徵。

恢復力是指物質的「彈性」，並且在移除力時恢復到其原始形狀的變形稱為「彈性變形」。然而，當力（更精確地，應力）施加了超過該材料的限制，所以留下了（更確切地說，應變）甚至不包括力變形。該特性稱為「塑性變形」，由於塑性的性質而不能恢復到原始狀態的變形稱為「塑性變形」。彈性變形中變形保持的最大應力稱為「彈性極限」。由於彈簧是回到原來的前提,使用的塑性變形是用在受力範圍內適用於彈簧的理想,一般不超過彈性極限。

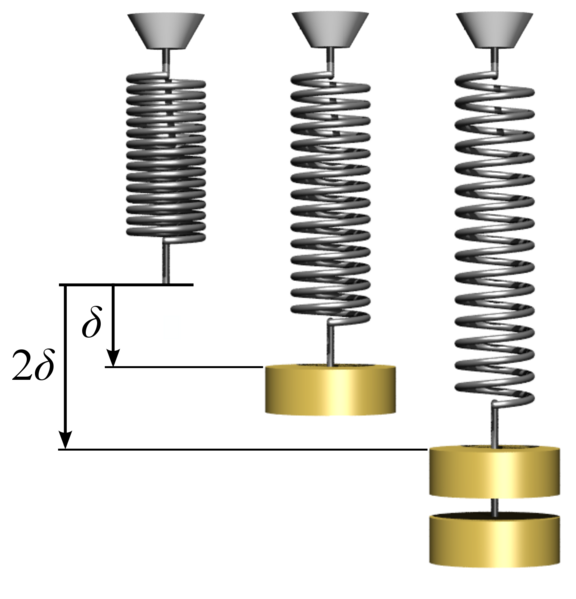
對於線性特徵彈簧，偏轉與負載成比例。

彈簧的變形和變形量為「彎曲」。有兩種類型的計量單位的偏轉，位移（長度變化）和旋轉角度（扭轉角度和彎曲角度的變化）。在壓縮螺旋彈簧中，利用長度變化的事實，偏轉單位由位移表示。對應於物理偏轉量，可以想到幾種引起偏轉的載荷。如果是位移，則是結構荷重（純力），如果是扭轉角，則考慮扭轉力矩。一些實際的彈簧會引起復雜的偏轉以及位移和旋轉變形。

彈簧的基本特性和功能之一是這種載荷和撓度具有一定的關係。由彈簧指示的載荷和撓度之間的關係稱為「彈簧特性」，「載荷 - 撓度特性」，「載荷特性」等。彈簧最常用的彈簧特性通常是線性的。偏轉並線性負載比例，它增加和在10中的彈簧減小公斤的重量掛在彈簧1厘米的伸長率，並且使得懸浮延伸20kg的重量2厘米。這種關係也被稱為「胡克定律」。對於作為線性特性的彈簧，負載和偏轉之間的關係由下式表示。(圖文自維基百科)